Nghiên cứu mới từ UC Berkeley kết hợp GPT với Prolog để cải thiện đáng kể khả năng giải toán

• Các mô hình ngôn ngữ lớn (LLM) như GPT thể hiện hiệu suất cao trong nhiều lĩnh vực, nhưng vẫn gặp khó khăn trong suy luận một cách đáng tin cậy và linh hoạt.

• Hạn chế này có thể do cách hoạt động của kiến trúc transformer, giải quyết vấn đề từng bước và dự đoán từ tiếp theo trong chuỗi, hạn chế khả năng quay lui và sửa lỗi.

• Các nhà nghiên cứu từ Đại học California, Berkeley đề xuất tích hợp một mô-đun suy luận suy diễn đáng tin cậy vào quy trình suy luận của họ.

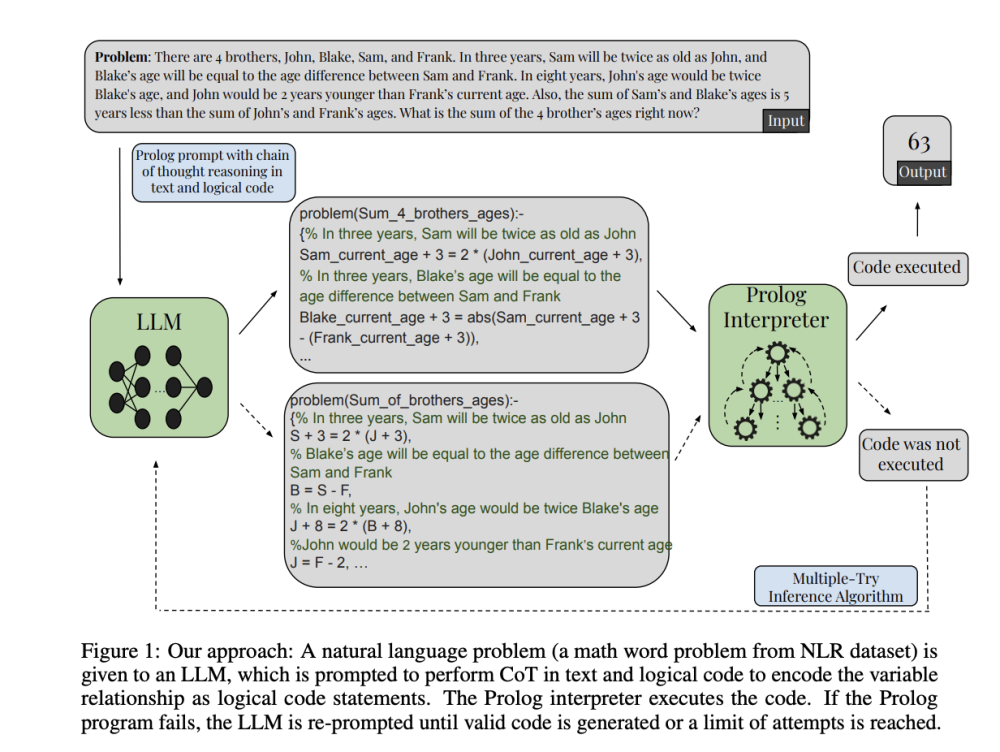
• Phương pháp này yêu cầu mô hình mã hóa các ràng buộc và mối quan hệ thành một tập hợp các câu lệnh mã Prolog trong các biến được giải thích trong phát biểu bài toán.

• Prolog đánh giá mã được tạo ra bằng kỹ thuật suy diễn để đưa ra câu trả lời xác định cho vấn đề.

• Phương pháp này cũng phản ánh kiến trúc con người có thể có với các hệ thống ngôn ngữ và suy luận riêng biệt.

• Các nhà nghiên cứu cũng giới thiệu bộ dữ liệu Suy luận Phi tuyến tính (NLR), một bộ dữ liệu mới để kiểm tra khả năng xử lý suy luận toán học của LLM.

• Bộ dữ liệu NLR đảm bảo không được đưa vào tập huấn luyện của các mô hình hiện tại và mỗi bài toán đòi hỏi một mô hình suy luận độc đáo và sáng tạo để giải quyết.

• Bộ dữ liệu này chứa các bài toán ràng buộc độc đáo, bài toán toán có lời và các bài toán liên quan đến hướng dẫn thuật toán để cập nhật mô hình trò chơi.

• Để chứng minh ảnh hưởng của sự rối rắm biến đối với hiệu suất của mô hình, các trường hợp có cấu trúc và mô hình suy luận tương tự được tạo ra nhưng với số lượng biến rối rắm khác nhau.

• Khả năng giải quyết các bài toán này của GPT-4 giảm đáng kể khi số lượng biến rối rắm tăng lên. Nó thất bại trong việc giải quyết các bài toán liên quan đến 4 biến rối rắm khi được cung cấp CoT tiêu chuẩn trong văn bản.

• Hai thí nghiệm khác được thực hiện trên bộ dữ liệu NLR sử dụng GPT-3.5 Turbo và GPT-4. Loạt thí nghiệm đầu tiên so sánh hiệu suất trung bình của mô hình với đường cơ sở nhắc CoT chỉ bằng văn bản trên tất cả các bài toán.

• Phương pháp kết hợp này cải thiện đáng kể hiệu suất của LLM trong các tác vụ suy luận toán học.

📌 Nghiên cứu từ UC Berkeley kết hợp GPT với Prolog giúp cải thiện khả năng giải toán của AI. Bộ dữ liệu NLR mới được tạo ra để đánh giá suy luận phi tuyến tính, với 100 bài toán độc đáo. Phương pháp này khắc phục hạn chế trong dự đoán từ tiếp theo của LLM.

https://www.marktechpost.com/2024/07/22/this-ai-paper-from-uc-berkeley-shows-how-interfacing-gpt-with-prolog-reliable-symbolic-system-drastically-improves-its-math-problem-solving-abilities/